An interview question from baidu

流传的一道百度面试题

#include <stdio.h>
int main() {
    double a = 10;
    printf("a = %d\n", a);
    return 0;
}
grxer@grxer ~/D/s/NEMU [1]> gcc -m32 -g -o  test test.c
test.c: In function ‘main’:
test.c:4:18: warning: format ‘%d’ expects argument of type ‘int’, but argument 2 has type ‘double’ [-Wformat=]
    4 |     printf("a = %d\n", a);
      |                 ~^     ~
      |                  |     |
      |                  int   double
      |                 %f
grxer@grxer ~/D/s/NEMU> ./test
a = 0    
grxer@grxer ~/D/s/NEMU> gcc  -g -o  test test.c
test.c: In function ‘main’:
test.c:4:18: warning: format ‘%d’ expects argument of type ‘int’, but argument 2 has type ‘double’ [-Wformat=]
    4 |     printf("a = %d\n", a);
      |                 ~^     ~
      |                  |     |
      |                  int   double
      |                 %f
grxer@grxer ~/D/s/NEMU> ./test
a = 1853816616
grxer@grxer ~/D/s/NEMU> ./test
a = -600037016

IA-32上运行时, 打印结果为a=0; 在x86-64上运行时, 打印出来的a是一个不确定值

WHY?

IEEE 754

先复习一些IEEE 754浮点数

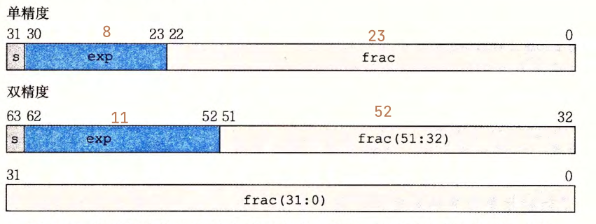
image-20230420111646829

单精度 1位符号位(sign) 8位阶码(exponent) 23位有效数(significand)

双精度 1 11 52

  • 规格化的值

    • exp阶码位域既不是全0也不是全1

    • 阶码字段是有偏置的有符号整数 E=e-Bias ps:专业术语叫做移码，这种偏置给浮点数的比较带来了巨大方便

      • e是exp表示的无符号数
      • Bias是偏置值=2k-1-1 单精度为28-1-1=127 双精度为211-1-1=1023
      • 所以单精度指数范围为 1-127~254-127即-126~+127 双精度为-1022~+1023 (exp阶码位域既不是全0也不是全1)

    • significand位总是1.开头，也就是有效数大于等于1且小于2，所以不记录1,只记录小数点后面的值

    • 值Value=$(-1)^{s}2^{exp-Bias}*(1+.frac)$

  • 非规格化的值

    • exp阶码位域全为0
    • 阶码值E=1-Bias
      • 32位-126，64位-1022
    • 有效数0.开头，也就是有效数小于1且大于等于0
    • 非规格化浮点值的绝对值小于所有的规格化浮点数的绝对值
    • 有效数全为0时，符号位决定了+0,-0的表示
    • 非规格化浮点填补绝对值意义下最小规格数与零的距离(太小的浮点数规格化的exp位不够用)，最大的非规格数等于最小的规格数

  • 特殊值

    • exp阶码全为1
      • 有效数全为0时，表示无穷inf(infinity) 符号位决定+inf，-inf 非0浮点数和整数不一样，他是可以除以0的，得到inf
      • 有效数不全为0，表示Nan(not a number)，有时候利用Nan和其他任何数比较返回false的特性可能造成一些支付逻辑上的漏洞

  • 对于nan的一些特性 x：including NaN and ±∞

    Comparison NaN ≥ x NaN ≤ x NaN > x NaN < x NaN = x NaN ≠ x
    Result False False False False False True

在线转换

https://www.toolhelper.cn/Digit/FractionConvert

https://www.h-schmidt.net/FloatConverter/IEEE754.html

IA-32

对于ia32的结果我们并不感到奇怪，

double的10.00先手动转一下吧，写为二进制1010.00，然后需要左移三位才能1.0开头，即1.010*23,所以S=0，E=1023+3=100 0000 0010b significand=010，组合起来就可以了

0 10000000010 0100000000000000000000000000000000000000000000000000 hex=0x4024000000000000

32位参数都是在栈上(除非你用fastcall的调用约定，C/C++默认的函数调用协议的_cdecl)，我们的浮点数有专门的处理单元，寄存器，和指令集

IA-32采用了x87 FPU的指令集来处理浮点数

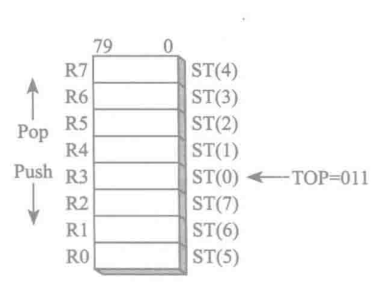
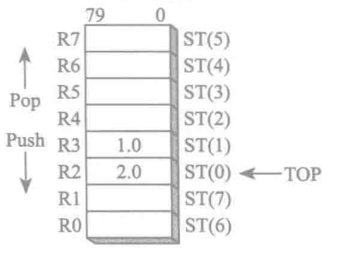
FPU有8个独立的可寻址的80位数据寄存器R0~R7，这组寄存器叫做寄存器栈，FPU状态字中名为TOP的3位字段给出了当前栈顶的寄存器编号，入栈top-1，出栈+1，7如果再出栈top会回到R0，如果覆盖掉原有数据会产生浮点数异常

image-20230418232538589

st0总是表示栈顶，即top所指即st0

image-20230419133610761

浮点数在进栈会拓展到80位，出栈时从80位进行转换

为什么会用栈呢，学过数据结构的可能已经猜到了，这里是用后缀表达式通过栈来来进行的运算

但是他还是把参数压栈了

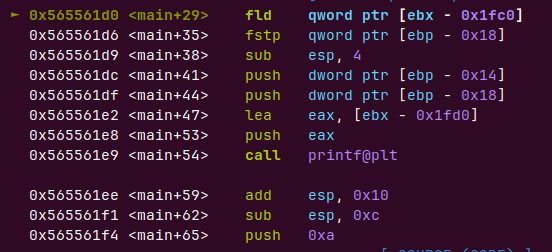
image-20230420110749224

典型_cdecl特征 参数右向左入栈，外平栈(调用者平栈)，还分了两次把8自己字节的double压栈，其实我们在骗他玩，哈哈

image-20230418113446986

此时的栈按四字节int输出0没问题

x86-64

顺便说一下为什么不叫IA-64架构，害，因为IA-64的名字被安腾架构占去，但是由于不兼容32位没流行起来，amd64位兼容32位流行起来，随后一般intel被迫追随叫x86-64

64位采用寄存器传参，x64用了SSE指令集，这里要细说起来内容挺多的，推出的主要原因是为了提高3d游戏性能

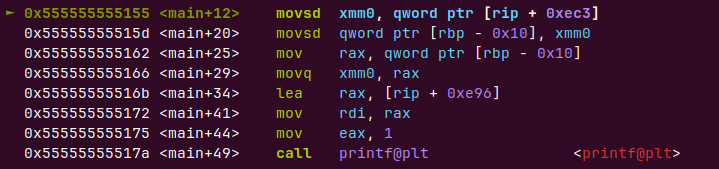
image-20230418140620437

直接把浮点数放到了xmm0寄存器，如果取的话也直接去这里取(rip的相对寻址rip是执行这条指令过后的rip)

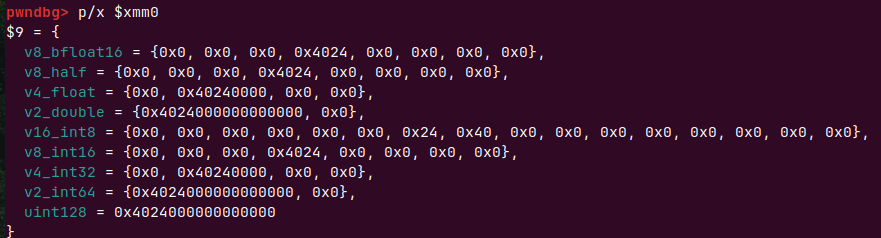
image-20230418140809555

我们%d会在常规的rsi低四字节做参数

image-20230418141359969

FFFFDF48四个字节，这次就输出-8,376

image-20230418141756625

所以这就可以有些很有意思但可能在初学c语言的人看来很奇怪的事情，比如下面两个传参都打印出正确结果

#include <stdio.h>
int main() {
    int x = 12;
    double y = 6.666;
    printf("%d,%f\n", x, y);
    printf("%d,%f", y, x);
    return 0;
}
grxer@grxer ~/D/s/NEMU> gcc -g -o  test test.c
test.c: In function ‘main’:
test.c:8:14: warning: format ‘%d’ expects argument of type ‘int’, but argument 2 has type ‘double’ [-Wformat=]
    8 |     printf("%d,%f", y, x);
      |             ~^      ~
      |              |      |
      |              int    double
      |             %f
test.c:8:17: warning: format ‘%f’ expects argument of type ‘double’, but argument 3 has type ‘int’ [-Wformat=]
    8 |     printf("%d,%f", y, x);
      |                ~^      ~
      |                 |      |
      |                 double int
      |                %d
grxer@grxer ~/D/s/NEMU> ./test
12,6.666000
12,6.666000⏎